组合变换

连接矩阵的优点是可以使用这些矩阵单独操作. 多个变换依然是一个矩阵. 连接矩阵不可交换，因为矩阵乘法不具有交换性.

X3=RX2 X2=SX1

X3=R(SX1)=（RS)X1

X3≠SRX1

逆变换：

方法1 求相乘结果的逆矩阵

方法2 求每个变换的逆矩阵，同时交换位置

也就是最后一个变换必须最先解除

M=M1M2M3

M-1=,M3-1M2-1M1-1

三维旋转

回顾二维矩阵

旋转矩阵是正交的 即R^TR=E

三维空间

二维旋转可以看成围绕Z轴的特殊旋转，因为Z轴保持不变

因此矩阵可看成

 

X坐标和Y坐标和二维一样。

相似的，关于X轴的旋转，矩阵如下：

 

同理得关于Y轴矩阵

因为Y等于Z叉乘X，矩阵稍有不同

 

所有这些矩阵都是正交的

我们可以把矩阵的每一行当作一个单位向量

 

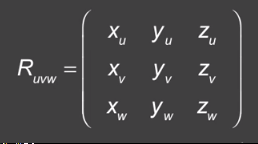
u=xuX+yuY+zuZ

v=xvX+yvY+zvZ

w=xwX+ywY+zwZ

向量u是新坐标系的坐标轴

由此可推导出，当给定了3个正交向量，正交就意味着

互相点成为0，并且u v w 都是单位向量

所以，给定任意的这样三个向量，就可以确定标准的XYZ坐标系下的一个旋转。

通过这些向量我们可以构建一个旋转矩阵。

还有一种方式，就是旋转矩阵乘以点的形式

把点P映射到了新的坐标系中。

 

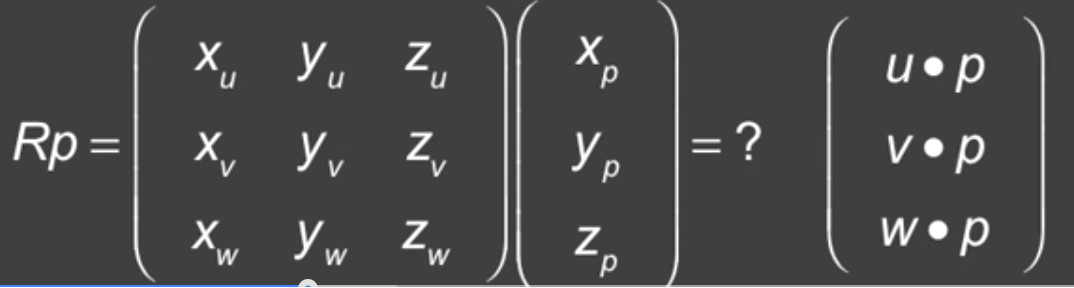
这是一个非常简单的三维旋转的解释。

你有一个新的坐标系，接着你在这个坐标系下得到P的点积。